Nghiên cứu xác định các hệ số lực khí động của xe du lịch

1. GIỚI THIỆU

Gió ngang ổn định có giá trị và phương của vận tốc không thay đổi theo thời gian. Khi xe du lịch chuyển động trong điều kiện gió ngang ổn định, thân xe sẽ chịu tác động đồng thời từ 2 nguồn gió: nguồn gió do lực cản không khí do chuyển động dọc của xe (v_v) và nguồn gió ngang ổn định (v_w). Theo tác giả Hucho [1] sự tác động của 2 nguồn gió trong điều kiện gió ngang ổn định sẽ tương đương với một nguồn gió có tốc độ v và góc nghiêng  (góc nghiêng giữa gió ngang và mặt phẳng đối xứng dọc của xe). Khi đó vận tốc v tương đương và góc xoay y của gió (so với phương chuyển động dọc x) được tính như sau:

           (1)

                  (2)

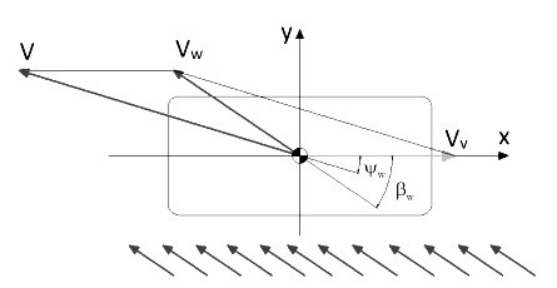
Hình 1. Mô hình gió ngang ổn định tác động lên xe du lịch

Thông số góc nghiêng  là rất quan trọng trong nghiên cứu ổn định chuyển động của ô tô trong điều kiện gió ngang. Các lực, momen khí động tác động lên xe du lịch trong trường hợp này được tính như sau:

                       (3)

                       (4)

                        (5)

                      (6)

                (7)

               (8)

Trong đó:

 C_D là hệ số lực dọc (theo trục x)

 C_S là hệ số lực ngang (theo trục y)

C_L là hệ số lực thẳng đứng (theo trục z)

C_R là hệ số mô men lắc ngang (quanh trục x)

C_P là hệ số mô men lắc dọc (quanh trục y)

C_Y là hệ số mô men quay thân xe (quanh trục z)

D là lực cản khí động (N)

S là lực bên khí động (N)

L là lực nâng khí động (N)

M_R là mô men lắc ngang (Nm)

M_P là mô men lắc dọc (Nm)

M_Y là mô men xoay thân xe (Nm)

 A là diện tích cản chính diện (m2)

 l là chiều dài cơ sở của xe (m)

V là vận tốc gió tương đương (m/s)

 r: mật độ không khí (kg/m3).

Các hệ số lực và mô men khí động (C_D, C_S, C_L, C_R, C_P, C_Y) được mô tả bằng các hàm toán học trong các nghiên cứu về ổn định chuyển động khí động từ các tác giả nước ngoài. Cụ thể các tác giả Milan Batista (2014), Barker (1986), Walczak (2016) sử dụng hàm số mũ, hàm sin ([2], [3], [5]) sử dụng hàm đa thức kết hợp với hàm lượng giác; tác giả Zhang (2018, [4]) sử dụng hàm đa thức bậc 2.

Trong bài báo này, tác giả xây dựng hàm toán học bậc 3 để mô tả sự phụ thuộc của các hệ số khí động theo góc nghiêng. Các hàm của hệ số khí động theo góc nghiêng được xác định từ các giá trị của hệ số khí động được tính toán bằng mô phỏng dựa trên phần mềm chuyên dụng.

2. TÍNH TOÁN CÁC GIÁ TRỊ HỆ SỐ KHÍ ĐỘNG BẰNG PHẦN MỀM CHUYÊN DỤNG

2.1. XÂY DỰNG MÔ HÌNH 3D

Trong bài báo này sử dụng xe Toyota Altis 2017 là xe tham khảo. Khi thực hiện mô phỏng, để phù hợp với khả năng tính toán của máy tính nhưng vẫn đảm bảo được tính đúng đắn, độ tin cậy và sự tương thích của bài toán nghiên cứu với thực tiễn, bài báo sử dụng các giả thiết sau:

- Mô hình vỏ xe là tuyệt đối cứng, không xảy ra sự biến dạng của vỏ xe trong suốt quá trình mô phỏng

- Bỏ qua quá trình trao đổi nhiệt giữa vỏ xe và không khí

- Bề mặt vỏ xe là bề mặt nhẵn, gầm xe được bọc phẳng (không xét đến các yếu tố khác của xe như: gương, gạt mưa, các gân, gờ, tay nắm cửa, ...)

Hệ tọa độ trong quá trình tính toán các lực, momen khí động là hệ tọa độ Đề các vuông góc, với gốc tọa độ trùng với trọng tâm của xe du lịch. Chiều “+” của các lực, mô men khí động được quy ước giống như hình 2.

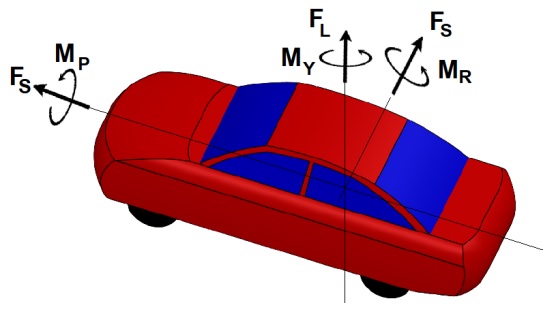
Hình 2. Mô hình 3D xe du lịch tham khảo trên hệ tọa độ

2.2. MÔ HÌNH DÒNG RỐI

Trong nghiên cứu khí động học ô tô, để mô tả dòng chảy không khí bao quanh vỏ xe các nhà nghiên cứu sử dụng phương trình Navier – Stoke. Với vận tốc dòng khí không lớn (hệ số M<0,3) nên có thể coi dòng khí chảy xung quanh vỏ xe ô tô là dòng không nén, khi đó ta có hệ phương trình vi phân sau:

       Để giải hệ phương trình vi phân này, phần mềm chuyên dụng sử dụng các mô hình dòng rối. Tác giả lựa chọn mô hình k-epsilon (2 eqn), Realizable với điều kiện biên “Non-Equilibrium Wall Functions Wall Treatmen”.

2.4. KẾT QUẢ MÔ PHỎNG

Các hệ số lực, mô men khí động được xác định từ các giá trị lực và mô men khí động theo các phương trình từ (3) đến (8). Các lực, mô men khí động được tính toán bằng phần mềm chuyên dụng có độ chính xác cao là Ansys Fluent [6] [7].

Các giá trị hệ số lực, hệ số mô men khí động theo các góc nghiêng được xác định theo bảng số 1 và bảng số 2.

Bảng 1. Hệ số lực khí động theo các góc nghiêng

Góc nghiêng	CD	CS	CL
100	0,325	0,485	0,019
200	0,347	0,956	0,778
300	0,306	1,465	1,373
400	0,225	1,940	1,674
500	0,084	2,273	1,750
600	-0,063	2,308	1,621
700	-0,125	2,151	1,116
800	-0,139	2,064	0,742

Góc nghiêng	CD	CS	CL
100	0,040	0,031	0,140
200	0,064	0,028	0,267
300	0,088	0,021	0,324
400	0,124	-0,040	0,336
500	0,170	-0,071	0,305
600	0,221	-0,095	0,275
700	0,216	-0,068	0,167
800	0,227	-0,051	0,021

3. XÂY DỰNG HÀM TOÁN HỌC CỦA CÁC HỆ SỐ KHÍ ĐỘNG

Khi xe du lịch di chuyển trong điều kiện gió tự nhiên, góc nghiêng  luôn luôn thay đổi. Vì vậy trong nhiều nghiên cứu về ổn định ngang các tác giả xây dựng hàm toán học của các hệ số khí động theo góc nghiêng  . Từ một số giá trị rời rạc các hệ số khí động như bảng 1, 2 tác giả lựa chọn hàm đa thức bậc ba để mô tả đặc trưng cho các hệ số khí động [5].

3.1. HỆ SỐ LỰC KHÍ ĐỘNG

Các hệ số lực khí động được minh họa như trên hình 4. Trong đó điểm hình vuông, nét liền biểu diễn giá trị mô phỏng và đồ thị hàm số của hệ số lực cản. Điểm hình tròn, nét chấm biểu diễn giá trị mô phỏng và đồ thị của hàm số hệ số lực bên. Điểm hình tam giác, nét đứt biểu diễn giá trị mô phỏng và đồ thị của hàm số hệ số lực nâng. Các hàm lực khí động được xác định như sau:

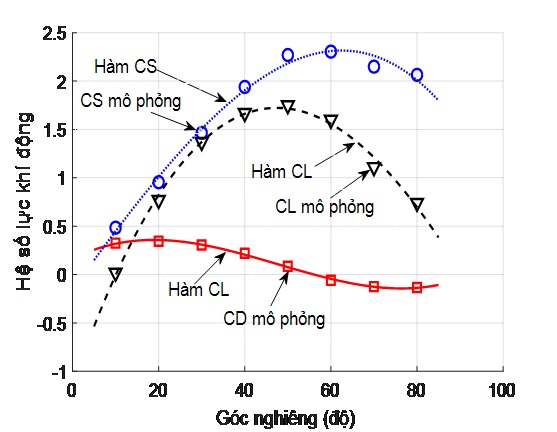
Hình 4. Các hệ số lực khí động

Việc xác định hàm toán học đặc trưng cho hệ số lực khí động từ các giá trị rời rạc trong bài báo là quá trình nội suy. Để đánh giá độ chính xác của quá trình nội suy xác định hệ số cản khí động, tác giả Zhang sử dụng chỉ số R-square (sai lệch bình phương trung bình) với tiêu chuẩn > 0,95. Các hệ số C_D, C_S, C_L trong bài báo có chỉ số R-square từ 0,9903 đến 0,9907 đều > 0,95.

Hệ số cản sẽ đạt cực đại C_Dmax = 0,362 tại góc nghiêng = 25,2⁰. Hệ số lực bên cực đại C_Smax = 2,331 tại góc nghiêng = 59,2⁰. Hệ số lực nâng cực đại C_Lmax = 1,80 tại góc nghiêng = 51,1⁰.

3.2. HỆ SỐ MÔ MEN KHÍ ĐỘNG

Các hệ số mô men khí động được minh họa như trên hình 5. Trong đó điểm hình vuông, nét liền biểu diễn giá trị mô phỏng và đồ thị hàm số của hệ số mô men lắc ngang. Điểm hình tròn, nét chấm biểu diễn giá trị mô phỏng và đồ thị của hàm số hệ số mô men lắc dọc. Điểm hình tam giác, nét đứt biểu diễn giá trị mô phỏng và đồ thị của hàm số hệ số mô men xoay thân xe.

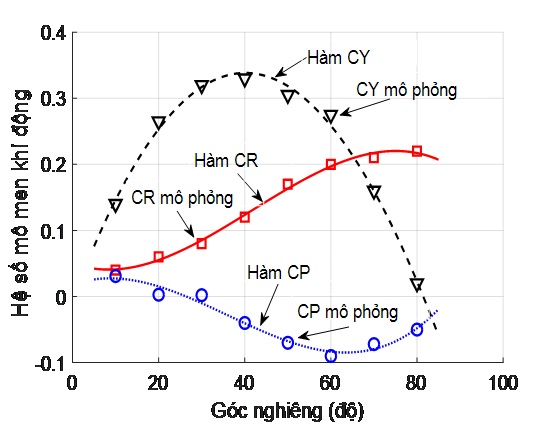
Hình 5. Các hệ số mô men khí động

Các hàm lực khí động được xác định như sau

Các hệ số mô men khí động C_R, C_P, C_Y trong bài báo có chỉ số R-square từ 0,9505 đến 0,995 đều > 0,95.

Hệ số momen lắc ngang cực đại C_Rmax = 0,22 tại góc nghiêng = 71,3⁰. Hệ số momen lắc dọc cực đại C_Pmax =  0,045 tại góc nghiêng = 10,2⁰. Hệ số mô men xoay thân xe cực đại C_Ymax =  0,349 tại góc nghiêng = 38,4⁰.

4. KẾT LUẬN:

Bài báo đã xác định hàm số của hệ số khí động theo góc nghiêng dựa trên các giá trị rời rạc từ mô phỏng số với độ chính xác cao. Kết quả của nghiên cứu có thể được sử dụng làm thông số đầu vào cho bài toán đánh giá sự ổn định chuyển động của xe du lịch trong các điều kiện gió ngang khác nhau.

TÀI LIỆU THAM KHẢO

[1]. W.H.Hucho, 1998. Aerodynamics of Road Vehicles: From Fluid Mechanics to Vehicle Engineering. SAE International.

[2]. Milan Batista, 2014.  A simple static analysis of moving road vehicle under crosswind.  J.    Wind Eng. Ind. Aerodyn. 128 105–113

[3]. Baker, 1986. A simplified analysis of various types of wind-induced road vehicle accidents. Journal of Wind Engineering and Industrial Aerodynamics, 22, 69-85.  

[4]. S Walczak, 2016. Analysis of vehicle dynamics under sadden cross
wind. IOP Conf. Ser.: Mater. Sci. Eng. 148 012030

[5]  Zhe Zhang, 2018. Combined simulation of heavy truck stability under sudden and discontinuous direction change of crosswind with computational fluid dynamics and multi-body system vehicle dynamics software. Advances in Mechanical Engineering, Vol.10(7) 1-10.

[6] Đo Tien Quyet, Nguyen Dinh Cuong, 2020.  Research calculation of drag coefficients by Ansys Fluent.  Tạp chí  nghiên cứu khoa học   Đại học Sao Đỏ số 2 - 2020, 28-32.

[7] Do Tien Quyet, 2020.  Study on computation of aerodynamic force acting on sedan in steady wind conditions. Tạp chí nghiên cứu khoa học Đại học Sao Đỏ số 4 -2020, 50-55.